삼각함수

삼각형

일직선 위에 놓여있지 않은 3개의 정점(Vertex)과 세개의 변(Edge)으로 이루어진 다각형.

세 변중 두개의 변이 이루는 각을 내각(Interior Angle)이라고 한다.

세개의 *내각의 합은 항상 180도이다.

 

직각삼각형

내각중 하나가 90도를 이루는 삼각형을 직각삼각형.

*빗변(Hypotenuse), 밑변(Adjacent), 높이(Opposite)이라고 변의 이름을 붙임.

 

피타고라스의 정리

직각삼각형의 두변을 알면 나머지 한변을 알수있는 공식.

h^2 = a^2 + o^2

 ​사인, 코사인, 탄젠트

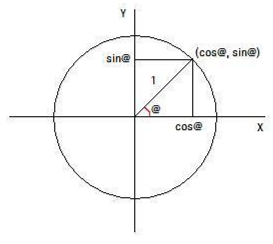
직각삼각형에서 변을 두 개 선택한 경우 두 변의 길이의 비율(삼각비)은 θ의 각도에 따라 변화한다.

위는 사인(sine)의 정의이다.

θ(세타)가 작아지면 높이가 작아져야하고 커지면 높이가 커져야한다는 것을 얼추 알 수 있다.

위는 코사인(cos)의 정의이다.

θ(세타)가 작아지면 밑변가 작아져야하고 커지면 밑변가 커져야한다는 것을 얼추 알 수 있다.

 

위는 탄젠트(tan)의 정의이다.

θ(세타)가 작아지면 높이가 작아져야하고 커지면 높이가 커져야한다는 것을 얼추 알 수 있다.

 

 

아크사인, 아크코사인, 아크탄젠트

θ = arcsin(sinθ)

θ = arccos(cosθ)

θ = arctan(tanθ)

 

삼각함수들의 역함수

 

삼각함수의 주기성

단위원

주기성

라디안

90º, 180º 의 “º(도)”처럼 다른 단위도 있다.

위 예시처럼 반지름의 길이만큼 원주가 됐을때의 각도를 1 라디안(radian)이라고 하고 이렇게 부르는 방법을 호도법이라고 한다.

 

180º는 3.14… 라디안정도가 되는데 이를 항상 3.14.. 이렇게 부르기 힘드니깐 π (파이)라고 대체한다.

그래서 90º는 π / 2, 180º는 π 에 대응된다. (육십분법 ↔ 호도법)

 

사인파, 코사인파, 탄젠트파